Lab 4: Digital Audio

Hours spent on lab: 9 Hours

Hours procrastinated: \(e^\inf\) Hours

Overview

In this lab, we shift away from Hardware Description Language and our FPGA. We begin to make some set-up files for our Microcontroller STM32L432KCUx to access its internal clock, GPIO clocks, and Timer clocks to generate electrical pulses and delays in the form of square waves.

Hardware Setup

I followed figure 9-5 on the LM386 datasheet using the audio amplifier. To create my breadboard:

Breadboard
Breadboard

Schematic

The schematic for the circuit includes the MCU, Piano switches, Push-Buttons, and the LM386 Audio Amplifier.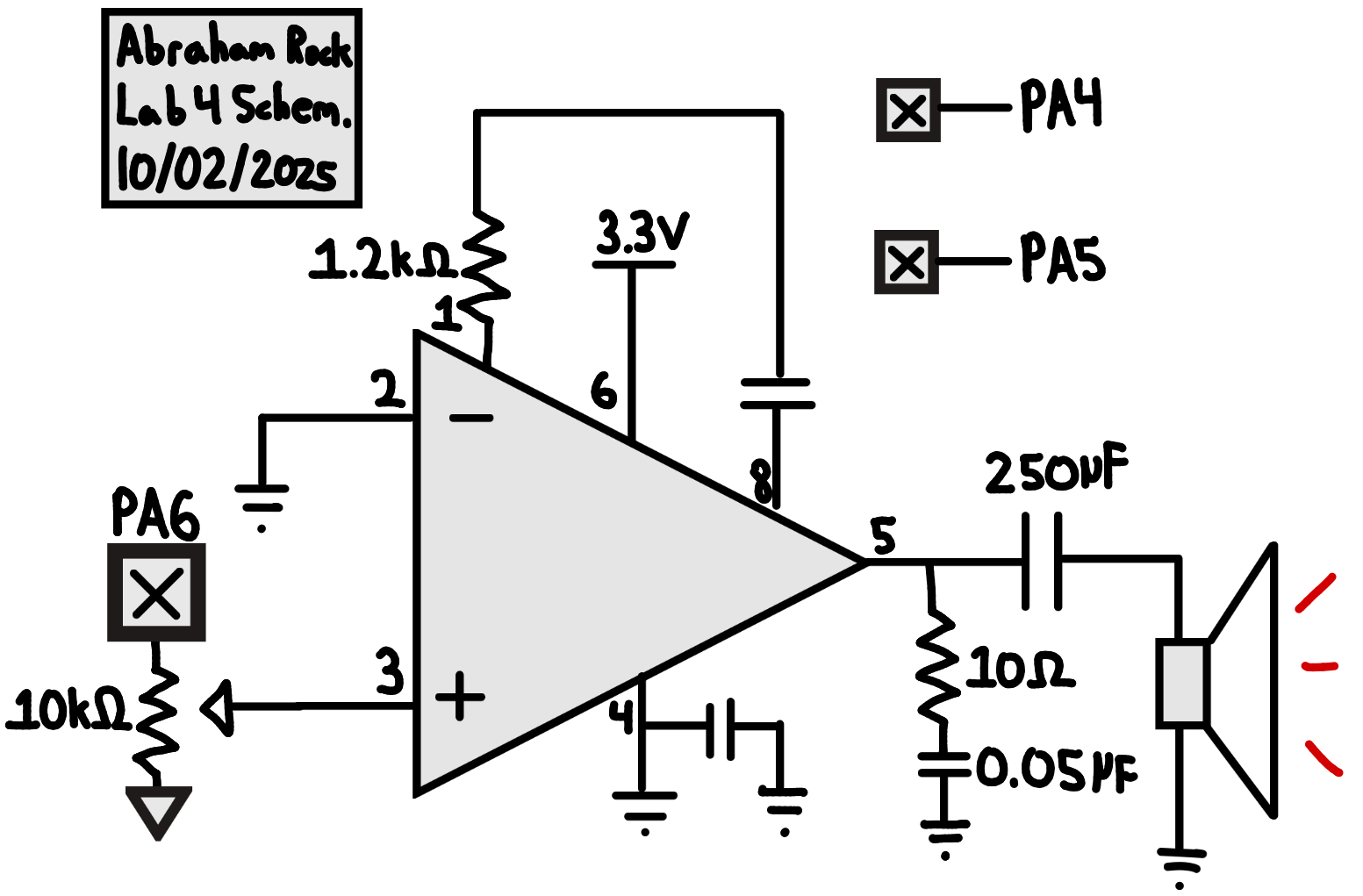
Schematic
Schematic

Calculations

Delay

Given the following formulas:

  • \(f_{timer}=\frac{f_{clk}}{PSC+1}\)
  • \(f_{reload}=\frac{f_{timer}}{ARR+1}\)
  • \(T=\frac{PSC+1}{f_{clk}}\times (ARR+1)\)

Hardcoding PSC for delay as 2500, we can use our first equation \(f_{timer}=\frac{80 * 10^6 Hz}{2501} \approx 31987.2 Hz\). We can then use our 3rd equation to see our minimum and maximum delay depending on what \(ARR\) is set as as the incrementer.

Minimum (ARR = 1): \(T=\frac{2501}{80 * 10^6 Hz}\times (2) \approx 62.5 \mu s\).

Maximum (ARR = 65635 = 0xFFFF): \(T=\frac{2501}{80 * 10^6 Hz}\times (65535) \approx 2.05 s\).

Pulse Width Modulation

Given the following formula:

  • \(f_{pwm}=\frac{f_{clk}}{(PSC+1)(ARR+1)}\)

Minimum (largest PSC and ARR): \(f_{pwm}=\frac{80 * 10^6 Hz}{65535^2} \approx 18.627 mHz\)

Maximum (smallest PSC and ARR): \(f_{pwm}=\frac{80 * 10^6 Hz}{2} = 40 MHz\)

So let’s go through some examples to see how accurate our production is even with the rounding and integer division taking place.

78 Hz (Eb2):

\(D = \frac{80*10^6}{78} \approx 1025641.03\).

So my code would choose a PSC Value of \(\frac{1025641.03}{65536} - 1 \approx 15.65 - 1\).

I use ceil to round numbers with a decimal of 0.5 or more to the next largest integer so we end up getting \(16 - 1 = 15\).

It would then calculate a ARR Value of \(\frac{1025641.03}{15 + 1} \approx 64102.56\).

I use round to bring down numbers with a decimal of less than 0.5 to the next smallest integer getting us \(64103\).

Then calculating \(f_{clk} = \frac{80*10^6 Hz}{PSC * ARR} = \frac{80*10^6 Hz}{16 * 64103} \approx 77.995\).

We have an error of \(\frac{77.995 - 78}{78} \approx -0.0064 \%\).

440 Hz (A4):

\(D = \frac{80*10^6}{440} \approx 181818.\overline{18}\).

So my code would choose a PSC Value of \(\frac{181818.\overline{18}}{65536} - 1 \approx 2.8 - 1\).

I use ceil to round numbers with a decimal of 0.5 or more to the next largest integer so we end up getting \(3 - 1 = 2\).

It would then calculate a ARR Value of \(\frac{181818.\overline{18}}{2 + 1} \approx 60606.06\).

I use round to bring down numbers with a decimal of less than 0.5 to the next smallest integer getting us \(60606\).

Then calculating \(f_{clk} = \frac{80*10^6 Hz}{PSC * ARR} = \frac{80*10^6 Hz}{181818} = 440.00044\).

We have an error of \(\frac{440.00044 - 440}{440} = 0.0001 \%\).

1568 Hz (G6):

\(D = \frac{80*10^6}{1568} \approx 51020.41\).

So my code would choose a PSC Value of \(\frac{51020.41}{65536} - 1 \approx 0.77 - 1\).

I use ceil to round numbers with a decimal of 0.5 or more to the next largest integer so we end up getting \(1 - 1 = 0\).

It would then calculate a ARR Value of \(\frac{51020.41}{0 + 1} \approx 51020.41\).

I use round to bring down numbers with a decimal of less than 0.5 to the next smallest integer getting us \(51020\).

Then calculating \(f_{clk} = \frac{80*10^6 Hz}{PSC * ARR} = \frac{80*10^6 Hz}{51021} \approx 1567.97\).

We have an error of \(\frac{1567.97 - 1568}{1568} \approx -0.0019 \%\).

Verification

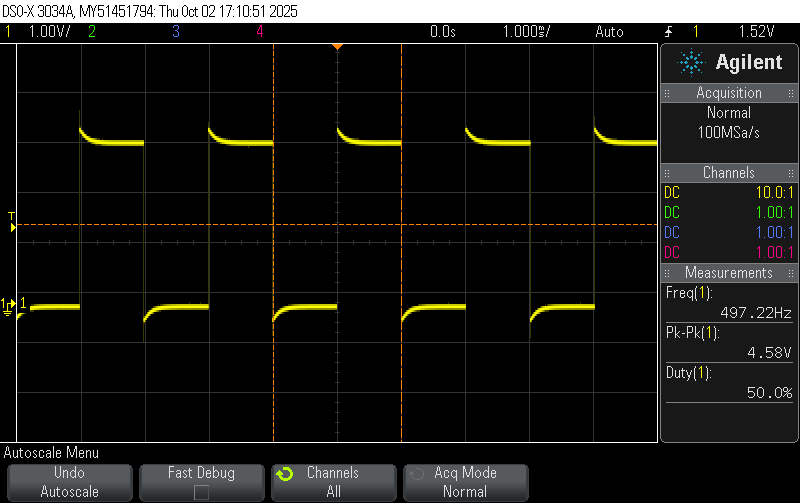
500 Hz Oscilloscope Trace
500 Hz Trace

Percent Error = \(\frac{497.22 - 500}{500} \approx 0.56 \%\)

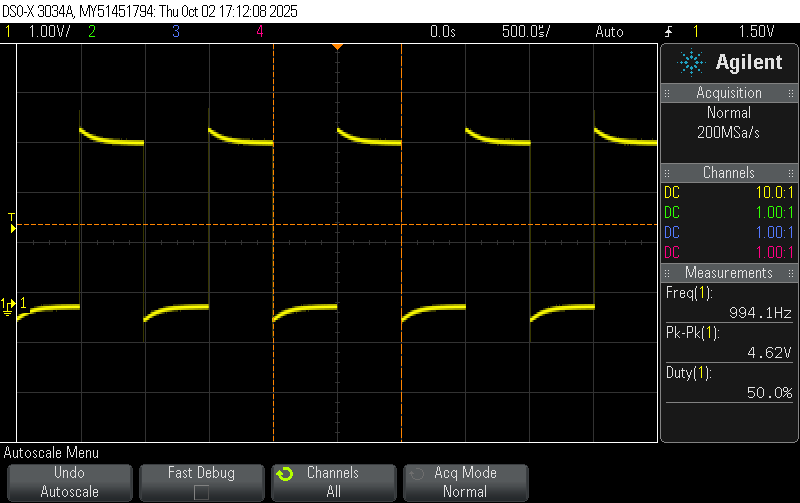
1000 Hz Oscilloscope Trace
1000 Hz Trace

Percent Error = \(\frac{994.1 - 1000}{1000} \approx 0.59 \%\)

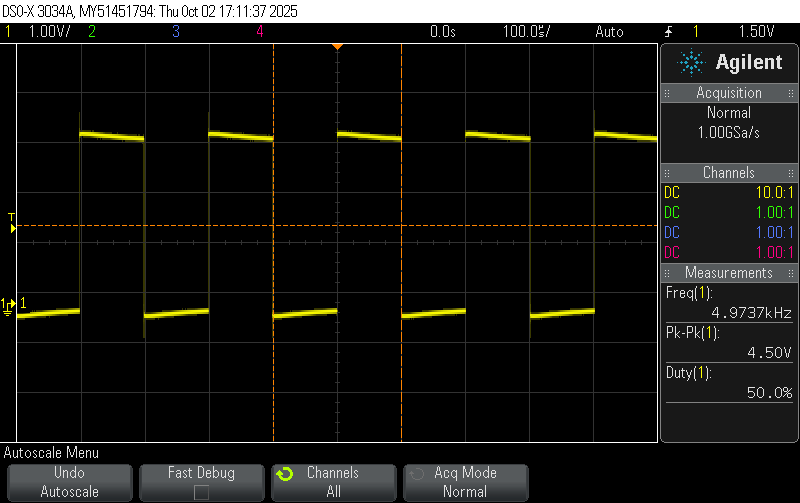
5000 Hz Oscilloscope Trace
5000 Hz Trace

Percent Error = \(\frac{4973.7 - 5000}{5000} \approx 0.53 \%\)

AI Prototype

This week I prompted Claude AI with “What timers should I use on the STM32L432KC to generate frequencies ranging from 220Hz to 1kHz? What’s the best choice of timer if I want to easily connect it to a GPIO pin? What formulae are relevant, and what registers need to be set to configure them properly?”. For additional context, I was able to upload the Datasheet and Reference Manual to the AI so it could potentially go through and not hallucinate registers.

Claude AI Response Summary

Recommended Timer: TIM2 (32-bit general-purpose timer)

  • Best for 220Hz-1kHz range due to 32-bit counter flexibility
  • 4 channels available for PWM output
  • Easy GPIO mapping via alternate functions

Key Formula: 

f_output = f_timer / ((PSC + 1) × (ARR + 1))

Where f_timer is typically 80 MHz, PSC is the prescaler value, and ARR is the auto-reload value.

Essential Registers:

  • TIMx_PSC - Prescaler (divides clock)
  • TIMx_ARR - Auto-reload register (defines period)
  • TIMx_CCRx - Capture/compare (sets duty cycle)
  • TIMx_CCMR - Set to PWM mode (OCxM = 110 or 111)
  • TIMx_CCER - Enable channel output
  • TIMx_CR1 - Enable counter

Example (440Hz): With 80 MHz clock, PSC=79, ARR=2272 gives 440.05 Hz

GPIO Connection: Configure pin alternate function per datasheet tables (e.g., PA0 = TIM2_CH1 with AF1)

I think it did a good job with this response. From my understanding of the reference manual, TIM2 is one of the more robust timers on our microcontroller and could definetley be used to produce a PWM signal.

Conclusion

The design worked as intended. You are able to trigger the given song: Fur Elise by the press of a button, and trigger my song of choice: Un Sospiro by clicking a switch.